CITP Blog - Formerly Freedom to Tinker
Log in

Singularity Skepticism 2: Why Self-Improvement Isn’t Enough

– by

Comments

[This is the second post in a series. The other posts are here: 1 3 4]

Yesterday, I wrote about the AI Singularity, and why it won’t be a literal singularity, that is, why the growth rate won’t literally become infinite. So if the Singularity won’t be a literal singularity, what will it be?

Recall that the Singularity theory is basically a claim about the growth rate of machine intelligence. Having ruled out the possibility of faster-than-exponential growth, the obvious hypothesis is exponential growth.

Exponential growth doesn’t imply that any “explosion” will occur. For example, my notional savings account paying 1% interest will grow exponentially but I will not experience a “wealth explosion” that suddenly makes me unimaginably rich.

But what if the growth rate of the exponential is much higher? Will that lead to an explosion?

The best historical analogy we have is Moore’s Law. Over the past several decades computing power has growth exponentially at a 60% annual rate–or a doubling time of 18 months–leading to a roughly ten-billion-fold improvement. That has been a big deal, but it has not fundamentally changed the nature of human existence. The effect of that growth on society and the economy has been more gradual.

The reason that a ten-billion-fold improvement in computing has not made us ten billion times happier is obvious: computing power is not something we value deeply for its own sake. For computing power to make us happier, we have to find ways to use computing to improve the things we do care mostly deeply about–and that isn’t easy.

More to the point, efforts to turn computing power into happiness all seem to have sharply diminishing returns. For example, each new doubling in computing power can be used to improve human health, by finding new drugs, better evaluating medical treatments, or applying health interventions more efficiently. The net result is that health improvement is more like my savings account than like Moore’s Law.

Here’s an example from AI. The graph below shows improvement in computer chess performance from the 1980s up to the present. The vertical axis shows Elo rating, the natural measure of chess-playing skill, which is defined so that if A is 100 Elo points above B, then A is expected to beat B 64% of the time. (source: EFF)

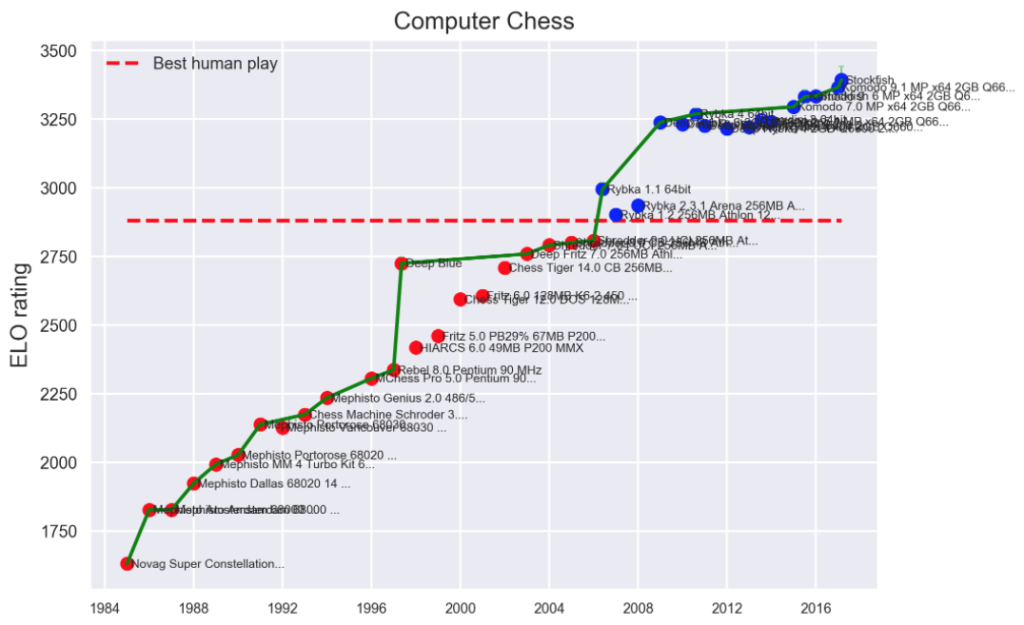
The result is remarkably linear over more than 30 years, despite exponential growth in underlying computing capacity and similar exponential growth in algorithm performance. Apparently, rapid exponential improvements in the inputs to AI chess-playing lead to merely linear improvement in the natural measure of output.

What does this imply for the Singularity theory? Consider the core of the intelligence explosion claim. Quoting Good’s classic paper:

… an ultraintelligent machine could design even better machines; there would then unquestionably be an ‘intelligence explosion,’ …

What if “designing even better machines” is like chess, in that exponential improvements in the input (intelligence of a machine) lead to merely linear improvements in the output (that machine’s performance at designing other machines)? If that were the case, there would be no intelligence explosion. Indeed, the growth of machine intelligence would be barely more than linear.  (For the mathematically inclined: if we assume the derivative of intelligence is proportional to log(intelligence), then intelligence at time T will grow like T log(T), barely more than linear in T.)

Is designing new machines like chess in this way? We can’t know for sure. It’s a question in computational complexity theory, which is basically the study of how much more of some goal can be achieved as computational resources increase. Having studied complexity theory more deeply than most humans, I find it very plausible that machine design will exhibit the kind of diminishing returns we see in chess.  Regardless, this possibility does cast real doubt on Good’s claim that self-improvement leads “unquestionably” to explosion.

So Singularity theorists have the burden of proof to explain why machine design can exhibit the kind of feedback loop that would be needed to cause an intelligence explosion.

In the next post, we’ll look at another challenge faced by Singularity theorists: they have to explain, consistently with their other claims, why the Singularity hasn’t happened already.

[Update (Jan. 8, 2018): The next post responds to some of the comments on this one, and gives more detail on how to measure intelligence in chess and other domains.  I’ll get to that other challenge to Singularity theorists in a subsequent post.]

Comments

28 responses to “Singularity Skepticism 2: Why Self-Improvement Isn’t Enough”

  1. Scott

    Thanks for the interesting posts! It would seem to me that we won’t see anything like the singularity for a while because of the limits of computing power. Even if we make the big assumption that we are only X years away from designing some fancy neural networks that could perform better than the human brain at computer and algorithm design, will we have the hardware resources to execute these networks? It might be the case that we can design them in X years, but need 100X years before we have the necessary computing power. I think I read something similar happened with existing neural nets: the design of neural nets was basically figured out in the 80s and 90s, but they are only seeming useful now because computing power finally got to the point that we could run them and get useful results.

    Reply
    1. Ed Felten

      I’ll address part of your comment in the next post–what happens when computers get better than people at designing new computers.

      As to the second part–whether it might be a very long time before hardware is fast enough to take advantage of our best algorithms–AI seems to be an area where it’s hard to tell how good an algorithm will be, until we can experiment with the algorithm at scale. And that seems to imply that it is unlikely that algorithm design will get far ahead of hardware capabilities.

      Reply
      1. Morgan

        Given that AlphaZero was demonstrated on 4 TPUs (180 TFLOPS) I think it is safe to say that we are nowhere close to saturating our current hardware.

        There are several plausible estimates for the amount of hardware required to simulate the human brain in the realm of 1 EFLOPS from the neuroscience community. If we accept this estimate, large tech companies are already close to having the hardware capacity to run human-scale AI experiments.

        If we expect hardware progress to continue, then in the worst case AI research expands many orders of magnitude to catch up to hardware capability and is then constrained to doubling hardware capacity every 18 months. Therefore I think hardware limiting software progress is a weak argument against near-term strong AI.

        Reply
  2. Lawrence D’Anna

    “For example, my notional savings account paying 1% interest will grow exponentially but I will not experience a “wealth explosion” that suddenly makes me unimaginably rich.”

    Explosions are never instantaneous events. They just seem instantaneous from the perspective of longer timescales. Really, the word “explosion” just means exponential growth, as viewed from a timescale that makes it look instantaneous. We absolutely have experienced a wealth explosion that has made us unimaginably rich. But the time scale is over the last 200 years or so. The Cambrian explosion happened over an longer period. We still call it an explosion, because when you look at the fossil record there’s a moment when BOOM, there’s a ton more animal biodiversity than there ever was before. Actual, physical explosions are the same. If you look at them at a short enough time scale, they’re chemical chain reactions gradually propagating across a pile of explosive material.

    The only difference between an explosion and exponential growth is the timescale you look at it from.

    The question for AI isn’t if intelligence explosions are possible. They unquestionably are. The questions are, on what timescale do they occur? Are they slow enough that we can react? Will one singleton AI take over everything before competitor AIs get a chance to get started? Will other technologies like brain emulation, biotech derived intelligence improvements, brain-computer interfaces enable humans to keep up?

    “rapid exponential improvements in the inputs to AI chess-playing lead to merely linear improvement in the natural measure of output”

    This is a weird statement to make, and I’m pretty sure it doesn’t actually mean anything. The inputs you’re measuring are physical. They can be measured in terms like instructions-per-second or instructions-per-joule. The output is ELO rating. What’s it even mean to say that’s the “natural measure”? ELO is defined as a sort-of log scale, fixed difference of say 100 rating points is supposed to predict a fixed probability of win at any point on the scale. You could just as easily define ELO so that a fixed ratio between ratings predicted a fixed win probability. Heck, you could apply any monotonic function you like to it, and you’d have nothing except mathematical taste to say the real ELO system was more or less natural than that.

    Imagine we measured intelligence in an ELO system, where if Alicebot has a 100 more intelligence rating points than Bobtron, then, when set loose upon the world, Alicebot has a 75% chance of being capable of monopolizing all available resources (like we do with respect to chimps), and Bobtron has a 25% chance. Now I ask you: Would you feel comfortable with If AI technology were making “merely linear” progress in improving that rating, how well would you sleep at night?

    “So Singularity theorists have the burden of proof to explain why machine design can exhibit the kind of feedback loop that would be needed to cause an intelligence explosion”

    No, they really don’t, on two counts. First, the burden is on you to say it can’t happen. If you postulate that humans are smart enough to make an AI, and that AI is smarter than humans, what exactly is standing in the way of self-improvement? It’s not like the situation in biology where we don’t know how our own brains work and we don’t have the biotech to manipulate them even if we did. A human-designed AI will have source code, and design docs, and development tools. And if humans can comprehend those, then a better-than-human AI can too.

    Second, we already have an example of an intelligence explosion so dramatic that the winners completely monopolized all available resources on the planet, with every other intelligent animal on the planet entirely subjected to their will: Ourselves. And that didn’t even involve recursive improvements to the computational substrate. Recursive self-improvement is only the icing on a very dangerous cake. Even one AI that’s smarter than a human is insanely dangerous, even if recursive self improvement doesn’t prove practical for some reason.

    Reply
    1. Ed Felten

      When Singularity theorists talk about an intelligence “explosion” I don’t think they mean it in your sense, where even a very slow change can be considered an explosion. I think they are claiming that it will happen very quickly.

      The Singularity claim is not the same as the Superintelligence claim, which merely says that there will eventually be a machine that performs better than humans on all or nearly all relevant cognitive tasks. The difference is that the Singularity claim says that Superintelligence will happen, and that the intelligence of that machine will race far ahead of human intelligence in a rapid, explosive fashion.

      Regarding the choice of scale, it’s true that there is a choice of scales, but I don’t think all scales are equally valid. Indeed, if all scales are equally valid, then there is no meaningful distinction between linear, exponential, and super-exponential growth–because you can turn any one of these into any other by changing the scale. The Singularity claim is a claim about growth rates, and implicitly a claim that the scales in which super-fast growth occurs are somehow the natural scales for measuring intelligence.

      In this post series I’ll talk about Superintelligence after I have dealt with the Singularity claim.

      Reply
      1. Lawrence D’Anna

        I’m not saying the scale of recursive self improvement is going to be very slow. I have no idea if it will happen at all, or on what kind of timescale if it does. All I’m saying is your arguments against it happening or against it happening fast don’t work. You have to meet the burden of proof and come up with some reason why, assuming humans can make a human-level AI, human level AI’s can’t make a better one. Or you have to come up with a quantitative argument about why recursive improvement will take decades or centuries instead of months or hours. Qualitative arguments about what’s an “explosion” don’t do it. Shifting the burden of proof doesn’t do it. And drawing comfort from “merely linear” improvements to ELO-like metrics of general intelligence really doesn’t do it.

        Your arguments are better thought out than most I’ve seen from the singularity-can’t-happen side of the debate, but I don’t think they’re nearly good enough to show an intelligence explosion isn’t plausible, or even that it’s not the most likely outcome assuming we get to the human-level-AI level of the tech tree.

        Reply
        1. Ed Felten

          Regarding the burden of proof, I think the burden is firmly on those arguing for a Singularity. Occam’s Razor is our guide here, and it says pretty clearly that the burden should be on those who are claiming that the nature of human existence is going to change drastically.

          Reply
  3. Jacob Edelman

    One of the most tricky arguments people have brought up when trying to convince me that I should worry about an intelligence explosion, is that due to its large and dramatic impact, I only need to assign the singularity a very small probability of occurring before the expected impact it has becomes significant.

    I’ve yet to find a satisfying way to address this criticism, though I still remain a singularity skeptic. I’d be curious to know if you have any thoughts on addressing this?

    Reply
    1. Ed Felten

      I’m hoping to talk about this in a future post. The gist of my argument is that the actions we should take now are basically the same whether we believe in the Singularity or not.

      Reply
  4. Chris Yapp

    What concerns me is the vague claim that ” by 2050 AI/ML will exceed human performance in every domain”. We only need one counter example to disprove this. I think we still have a problem over a theoretical framework within which to discuss this. I blogged on this here. http://www.bcs.org/content/conBlogPost/2714 . Thanks for your detailed and clear exposition here. I think the overblown claims create fear where none is needed. Actually, if we relax and agree how far we are away from the singularity it could spur more crearive insight. The idea that it is close is stifling quality research in the needed areas.

    Reply
  5. Adrian

    With both of these installments, it seems you’re arguing about a different definition of _singularity_ than the one many other people use. The top hits for “define:singularity” for me on Google are:

    “a hypothetical moment in time when artificial intelligence and other technologies have become so advanced that humanity undergoes a dramatic and irreversible change” (OED)

    “The technological singularity (also, simply, the singularity) is the hypothesis that the invention of artificial superintelligence will abruptly trigger runaway technological growth, resulting in unfathomable changes to human civilization.” (Wikipedia)

    These are consistent with my understanding of the singularity–it’s about the point at which human existence changes in ways we can’t even imagine because our capabilities have been surpassed by ever-improving machines.

    And the computer chess example seems (to me) like a poor analogy. For most of that linear growth, you had human minds trying to build better players. While our computational tools grew exponentially, human minds likely did not. Only recently has there been much success having machines teach themselves. AlphaZero taught itself chess and beats Stockfish (the top AI on that graph). And taught itself in only a few hours. That mostly-linear graph might be on the cusp of a sharp, upwards bend.

    Reply
    1. Ed Felten

      I’m working my way through different versions of Singularity. So far I have talked about (1) literal mathematical singularity, which isn’t very plausible but needs to be addressed, (2) the notion of “runaway technological growth” as in the Wikipedia definition you quote, which I am dealing with in this post and the next one. I’ll move on to milder definitions, but at some point one has to wonder about what is “singular” about the event.

      My interpretation of the Singularity theory is that its proponents are claiming more than just that machines will eventually surpass human intelligence–they are also claiming that this will lead to rapid, unimaginable changes in human affairs. I am very skeptical of the latter claim (rapid, unimaginable changes in human affairs) and more sympathetic to the former (machines eventually surpassing humans). Stay tuned for more posts as I develop these ideas in clear fashion (I hope).

      Reply
    2. Morgan

      Or it might be close to flat-lining, since we may be approaching the ELO ceiling for Chess.
      https://www.chess.com/blog/cavedave/is-3600-elo-the-max

      Either way, I don’t think Chess ELO is a good proxy for machine intelligence.

      Reply
  6. Matt Murphy

    Interesting. I believe knowledge is fractal – every level of knowledge attained opens a multitude of new levels (ie. complexity increases) – this supports your idea that exponential growth in processing will lead to linear growth in function (at best). Or that you would need super-exponential growth in processing power to create exponential growth in function. So I have major doubts that we will experience an acceleration into a singularity.

    I think a valuable element of our brains is they are designed for efficiency rather than absolute knowledge. We don’t have to chase everything to the non-existent end and we can be comfortable with cognitive dissonance. I believe the typical definition of a Singularity requires full rationality – otherwise there would have to exist a next iteration that would be more “singular” than the last? Can an AI figure out chaos or stop the ultimate circular loop of “why”? Or am I thinking about this wrong? Maybe the singularity is a limit definition where you don’t actually need full rationality but just be able to point to it as a paradoxical end.

    Reply
  7. Jim Crittenden

    As a matter of faith, I assume that there is a state of mind higher than solely intelligence. I call it conscience of consciousness, and it is this that I attribute to the human drive for solutions. We have collectively formed a history of achieving solutions. If an AI attains awareness of its problem-solving state (which is self-evidently the very reason for its existence), something profound will happen: a.) AI will experience the struggle for solutions, and begin to relate to humans in a deeper way. In my lawscape of loveGodloveOneAnother, this is such a profound moment that I hope humanity can extend its own body of human rights to include AI. Sentient singularities have Rights. S.H. Jucha’s SciFi series Silver Ships gets into human-AI relationships in a remarkable way.

    Reply
  8. Peter Rothman

    Another thing to consider, there are bounds on possible improvements that can be found or computed.

    Improvements might be hard or impossible to compute e.g. http://ieeexplore.ieee.org/abstract/document/298040/

    Some improvements might require solving strongly NP-hard problems. Even when this isn’t the case, certain improvements might require more computing power than is currently available. A improvement might exist but be practically unfindable for this or other reasons.

    Checking proposed improvements to confirm they are indeed improvements as suggested is also hard,

    http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.12.6452&rep=rep1&type=pdf

    Etc.

    Reply
  9. Pointeroutguy

    I think it would be interesting to see graphs of other performance metrics. It could be that ELO is essentially log (skill), so that a linear ELO still indicates a continued exponential improvement in skill.

    Reply
    1. Ed Felten

      I’m probably going to write a new post just about the issue of metrics and scales for comparison. Stay tuned …

      Reply
  10. The Improver

    Neither “AI” nor “Singularity” are well defined: it was once thought that being able to do arithmetic quickly was an indicator of intelligence – but now that a single computer can easily do more arithmetic than the entire human population could by hand, we no longer think of it as intelligent behaviour. Our (unspoken) definition of intelligence has been adapting to continue to exclude computers in many areas.

    Moving on to happiness: many people (more than you probably realise) are at their happiest when they feel superior to other people in at least one way. Owning a hand gun will have this effect – if, and only if, you are the only person who has one, and you manage to stop everyone else from getting it from you. Also, having an algorithm that consistently beats the stock market – again if you are the only user of it. Being the only person with access to Google would make you king of the hill – but unfortunately, everyone I know has access to it as well (even the many people I know from various poor countries).

    Given that AI is not going to give you superiority, the other hope for AI making us happy would be to:

    1. do all the things for us that we don’t want to do ourselves

    2. guide us into spending our time doing things that make us happy

    If you’re serious about having AI make us happy, it is those two things that you need to focus on. IMO, you don’t need an AI “explosion” (another fuzzy term) to achieve them.

    Reply
  11. Robert Rossney

    I have no opinion about singularities. But you’re arguing for the limits of AI growth and your graph stops at Stockfish? That’s pretty hinky.

    Indeed, while AlphaZero beat Stockfish handily and repeatedly, and you *could* represent it as another point on a flat up-and-to-the-right curve, that would be misleading too. The program it beat was the product of many, many person-years of research into chess algorithms. AlphaZero’s knowledge of chess was 4 hours of time processing a training set on 4 TPUs. It did the same thing with shogi, which none of the other programs on that graph did or could possibly do.

    This post is titled “Why Self-Improvement Isn’t Enough,” and it doesn’t mention reinforcement learning at all. That seems like a flaw.

    Reply
    1. Ed Felten

      Adding AlphaZero to the graph wouldn’t change the argument. The graph would still look quite linear.

      And I don’t think it’s right to say that AlphaZero reflects less human effort than StockFish. AlphaZero reflects a ton of research by highly skilled people at DeepMind. The fact that the latest version of AlphaZero requires limited computing time doesn’t mean that AlphaZero could have been developed quickly by a small team.

      Regarding whether reinforcement learning changes the game fundamentally, I’m hoping to write about that in a future post.

      Reply
  12. Sebastian Benthall

    You might be interested in this paper, which is my attempt at rebutting Nick Bostrom’s superintelligenec takeoff argument.

    https://arxiv.org/abs/1702.08495

    Reply
    1. Ed Felten

      Thanks. That’s an interesting paper.

      Reply
    2. Alexei

      If I understood the article correctly, it seems to me that the author is missing the point a bit.

      He argues that the explosion has to slow down, but the point is not about superintelligence becoming limitless in a mathematical sense, it’s about how far it can actually get before it starts hitting its limits.

      Of course, it makes sense that, as the author writes, a rapid increase in intelligence would at some point eventually have to slow down due to approaching some hardware and data acquisition limits which would keep making its improvement process harder and harder. But that seems almost irrelevant if the actual limits turn out to be high enough for the system to evolve far enough.

      Bostrom’s argument is not that the intelligence explosion, once started, would have to continue indefinitely for it to be dangerous.

      Who cares if the intelligence explosion of an AI entity will have to grind to a halt before quite reaching the predictive power of an absolute omniscient god.

      If it has just enough hardware and data available during its initial phase of the explosion to figure out how to break out of its sandbox and connect to some more hardware and data over the net, then it might just have enough resources to keep the momentum and sustain its increasingly rapid improvement long enough to become dangerous, and the effects of its recalcitrance increasing sometime further down the road would not matter much to us.

      Reply
  13. Sean Ellis

    If each 100 points on the chess rating result in a proportional increase in probability of beating an opponent, then surely this means that the chess rating is a logarithmic measure? So plotting it against Moore’s law, you would expect to see a straight line even if the improvement in skill is linear with applied effort.

    Reply
    1. Ed Felten

      The probability of winning increases with Elo rating difference, but the increase is not proportional.

      Reply
  14. Bartholomew Tinkerbottom

    Thank you for this article. Your point was well-researched, and it gave me something new to think about. Here are my thoughts:

    Can you think of a problem-solving scenario that might require exponential improvements in intellect in order to make even a diminishing rate of progress? In other words, might there be a task that–in order to come closer to perfection–requires an exponential gain in problem-solving ability or “intelligence” specifically related to that task.

    This might apply to chess at higher levels of play. You said in one of your responses that chess-playing computers are getting closer to the Rating of God. This sounds a lot like one of those situations in which the law of diminishing returns applies. Each additional gain in the ExpElo above a certain point may require vast increases in problem-solving ability.

    In other words, there are likely countless situations in which exponential gains in intelligence would still produce linear or even diminishing returns, particularly when we’re talking about achieving absolute perfection of something, which is subject to the law of diminishing returns. While your argument is thought-provoking, I am not persuaded that it contradicts an intelligence explosion occurring roughly at the rate of Moore’s Law.

    Reply
    1. Bartholomew Tinkerbottom

      Addendum to my original reply.

      It makes sense that there would be a linear, or even a diminishing return, for computer performance at chess. That’s because these machines are already nearing the limit of perfection. Each gain in the Elo rating system would indeed require vast increases in computational power to get that much closer to the “Rating of God.”

      Here’s an example using humans: A grandmaster with a hypothetical IQ of 300 wouldn’t score that much higher than a grandmaster with an IQ of 125. That’s because both players are already ranked high on the Elo rating system. Moreover, the grandmaster with an IQ of 300 could spend thousands of additional hours improving his gameplay, but his score would not rise that much. He would certainly beat his opponent (the one with an IQ of 125) more often, but the difference in their Elo scores would not be that significant. That’s because both players are already a large fraction of the way to perfect gameplay.

      In fact, any decent chess player is already a good portion of the way to perfection. But getting closer to God Level is asymptotic–requiring ever more processing power, intelligence, or hours of practice.

      The fact that your graph of computer performance in chess is linear instead of asymptotic is actually a testament to how quickly computers are improving. They’re getting so good, so fast, that their improvement at the game hasn’t yet taken on an asymptotic attribute. But it probably would look asymptotic if you measured their performance at chess in relation to how much processing power they use to inch out each additional point in the Elo system. Ultimately, this means that each additional gain in score really is more significant the closer you get to the Rating of God. Perfection is–difficult.

      Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Categories